前言

Transformer 完全基於 Attention 注意力機制的架構。Attention 原先是被應用在 RNN，之後 Google 所提出的 Transformer 保留了原先 Attention 的優勢並移除了 RNN 的架構。Transformer 是一個蠻新的模型，最先由 2017 年被 Google 所提出一篇叫 Attention is all you need 的論文。

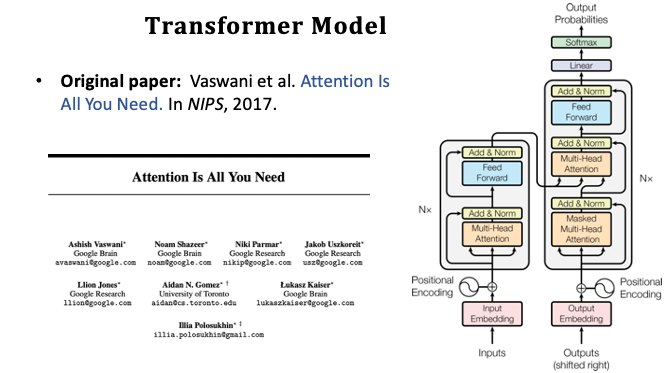
Transformer 是一種 Seq2seq 的模型，他有一個 Encoder 和 Decoder 並且非常適合做機器翻譯。另外在 Transformer 中拋棄了 RNN 循環神經網路的架構。Transformer 僅保留了 Attention 機制以及全連接層網路，實驗結果並優於 RNN+Attemtion 的架構。目前最新的機器翻譯研究已經很少人用 RNN 模型了，當今業界大多使用 Transformer + Bert 模型。

• Transformer is a Seq2Seq model.
• Transformer is not RNN.
• Purely based attention and dense layers.
• Higher accuracy than RNNs on large datasets.

重新審視 Attention + RNN

這裡來思考一個問題。當我們把 RNN 去掉只保留 Attention，僅利用 Attention 搭建一個神經網路用來取代 RNN。那我們該怎麼做呢？接下來我們會來詳細討論，從零開始基於 Attention 搭建一個神經網路的整個流程。首先在本篇文章我們先將之前學過的 RNN + Attention 開始入手，再抽取掉 RNN 保留 Attention。然後搭建一個 Attention 與 Self-Attention 網路層。下一篇文章會再將這些概念組裝起來，搭建一個深度的 Seq2seq 模型。搭出來的模型就是當今最紅的 Transformer。

Attention for Seq2Seq Model

RNN 的 Attention Ｑ、K、V 計算

在前篇文章有提到 RNN 模型的進化，最終使用 Attention 機制來改善 RNN Seq2seq 的模型。所謂的 Seq2seq 是指有一個 Encoder 和一個 Decoder。Encoder 的輸入是有 m 個時間點的輸入X₁~X_m，每個一個輸入都是經過編碼過後的向量。Encoder 把這些輸入的訊息壓縮到隱藏狀態向量 h 中，其最後一個狀態 h_m 是看過所有的輸入後所壓縮的訊息。Decoder 所做的事情取決於你的任務是什麼，例如文字生成器。在 Decoder 中會依序產生出狀態 s，每個時間點會根據狀態生成一個文字。我們在把輸出的文字作為下一次的輸入x^‘，如果有 Attention 機制的話還需要計算 context vector(c)。每當計算出一個狀態 s 就要計算一次 c。

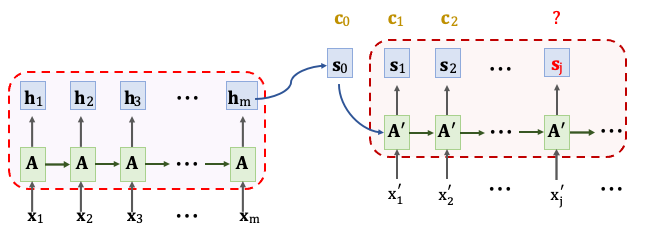
context vector(c) 計算方式是，首先將 Decoder 當前狀態 s_j 與 Encoder 所有狀態 h₁~h_m 做對比並用 align() 函數計算彼此間的相關性。把算出的 𝛼_ij 作為注意力的分數。 每計算一次 context vector 就要計算出 m 個分數，其表示 𝛼_1j ~ 𝛼_mj 。

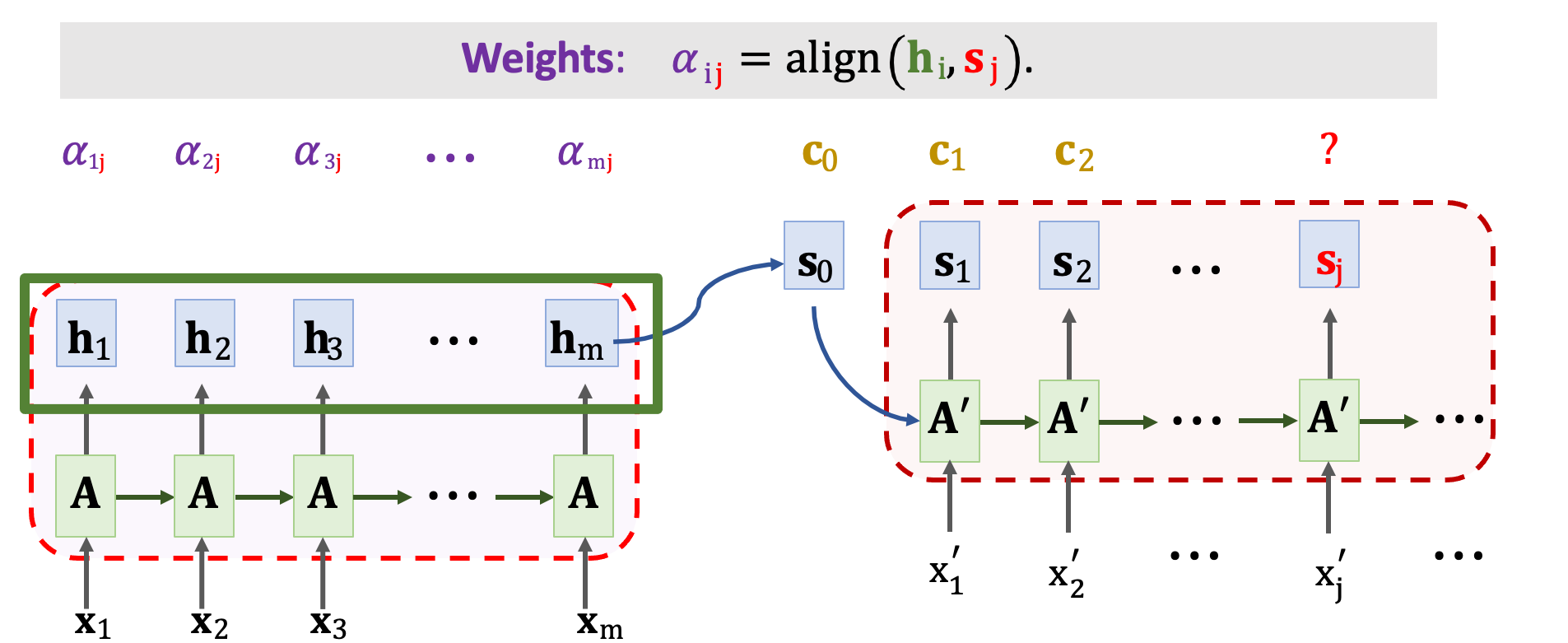
每一個 𝛼 對應一個狀態 h，以下我們具體的來看一下分數 𝛼 是如何被計算出來的。分數的計算是 h_i 和 s_j 的函數，首先我們必須計算 Q 和 K。把向量 h_i 乘上一個矩陣 W_K 得到 k_i。 另外把向量 s_j 乘上一個矩陣 W_Q 得到 q_j。這裡的矩陣 W_K 與 W_Q 是 align() 函數中可以學習的權重，必須經由訓練資料中去學習的。我們必須把 s_j 這一個向量與 Encoder 中的所有 h 去計算對比。有 m 個 h 向量因此會有 m 個 k，我們可以將 k₁~k_m 組成一個 K 矩陣。我們可以發現圖中綠色的 k_i 向量為 K 的每一行(col)。

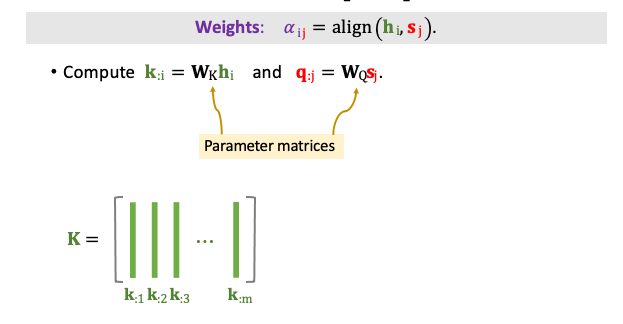
計算每個分數需要將 K 進行轉置並與 q_j 進行矩陣相乘的運算。輸出會是一個 m 維的向量。最後再使用一個 Softmax 函數將這些輸出的數值映射到 0~1 之間，並且這 m 個數值加總必為 1。此時的 𝛼_1j~ 𝛼_mj 為最終 q_j 所對輸入有感興趣的地方的分數。

剛才已經將 Decoder 狀態 s_j 還有 Encoder 狀態 h_i 分別做線性轉換，得到一組向量 q_j(Query) 與 m 個 k_i(Key)。我們拿一個 q_j 向量去對比所有 Key(K)，算出 m 個分數，這 m 個 𝛼 分數表示了 Query 與每一個 Key 的匹配程度。其匹配程度越高 𝛼 分數越大，同時也代表著模型需要更關注這些內容。除此之外我們還需要計算 Value，將 h_i 乘上一個矩陣 W_V 上 就能得到 v₁~v_m。這些合併起來就能用 V 表示，另外這裡的 W_V 也是可以透過機器學習的。

實際範例 Attention for Seq2Seq Model

剛剛已經講了 Q、K、V 這三種向量 在 RNN 架構中是如何被計算出來的。我們再回過頭看一下這個例子。首先我們先把 Decoder 目前狀態 s_j 乘上一個 W_Q 得到 q_j。

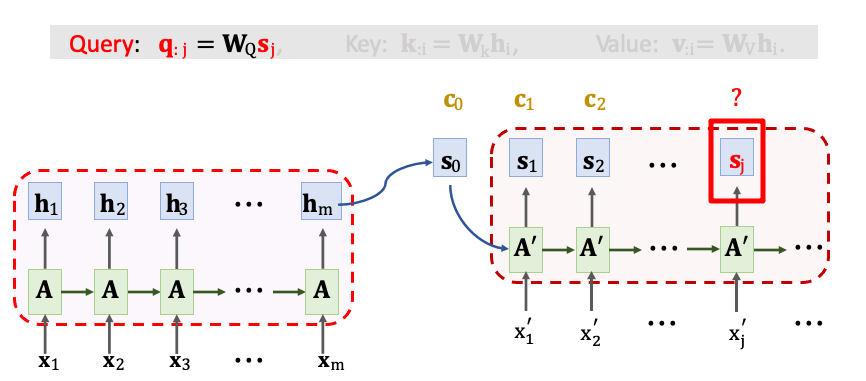
然後把 Encoder 所有 m 個狀態 h₁~h_m 乘上 W_K 映射到 Key 向量。

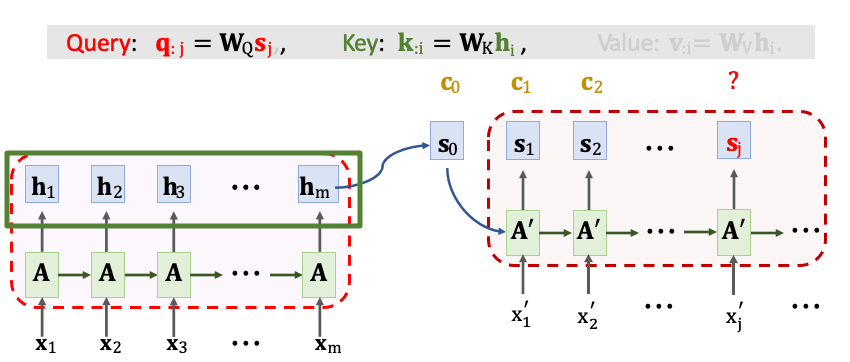
用矩陣 K 與向量 q_j 計算出 m 維的分數向量。a_1j~a_mj 對應每個 Encoder 的 h 向量。最後還要經過一個 Softmax() 即代表對輸入 x₁~x_m 所需要關注的分數。

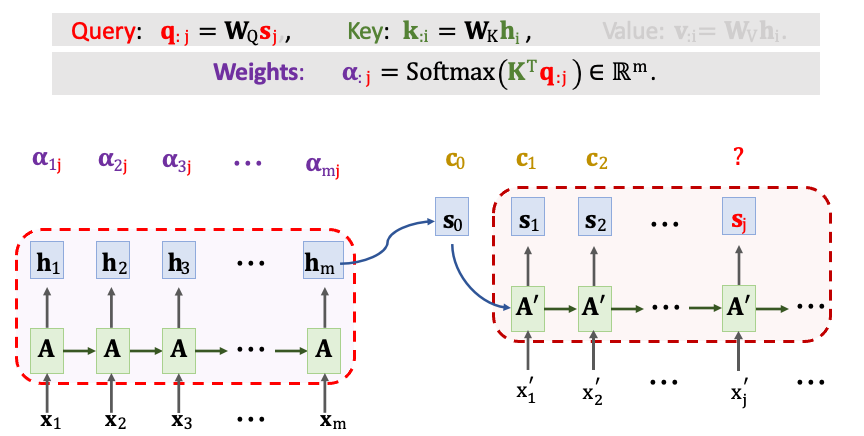
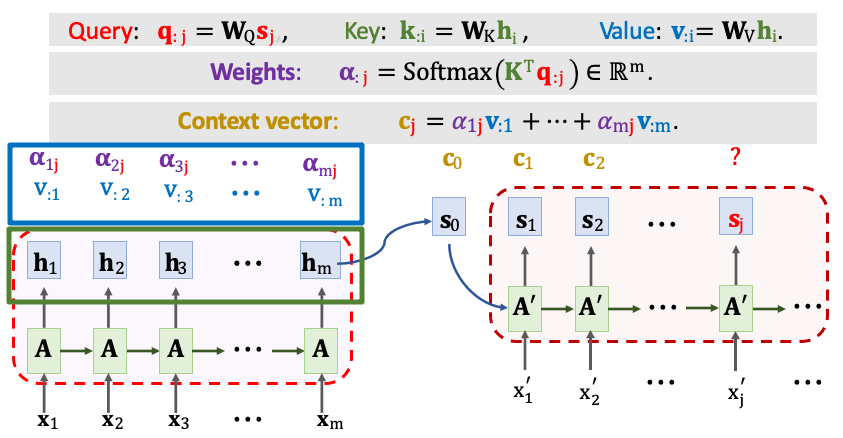
接下來計算 Value 向量 v_i，我們拿 Encoder 第 i 個狀態向量 h_i 與一個權重 W_V 做一個線性轉換得到 v_i。每一個 v_i 對應一個隱藏狀態 h。最終我們將會得到 m 個 𝛂 與 v，並做加權平均得到一組新的 context vector(c)。c_j 等於 𝛼_1j 乘上 v₁ 一直加到 𝛼_mj 乘上 v_m。 這種計算分數 𝛼 和 context vector(c) 的方法就是 Transformer 用的機制。

Attention without RNN

這一個部分我們來討論捨棄 RNN 只保留 Attention 的 Transformer，並得到一個 Attention 與 Self-Attention Layer。

Attention Layer

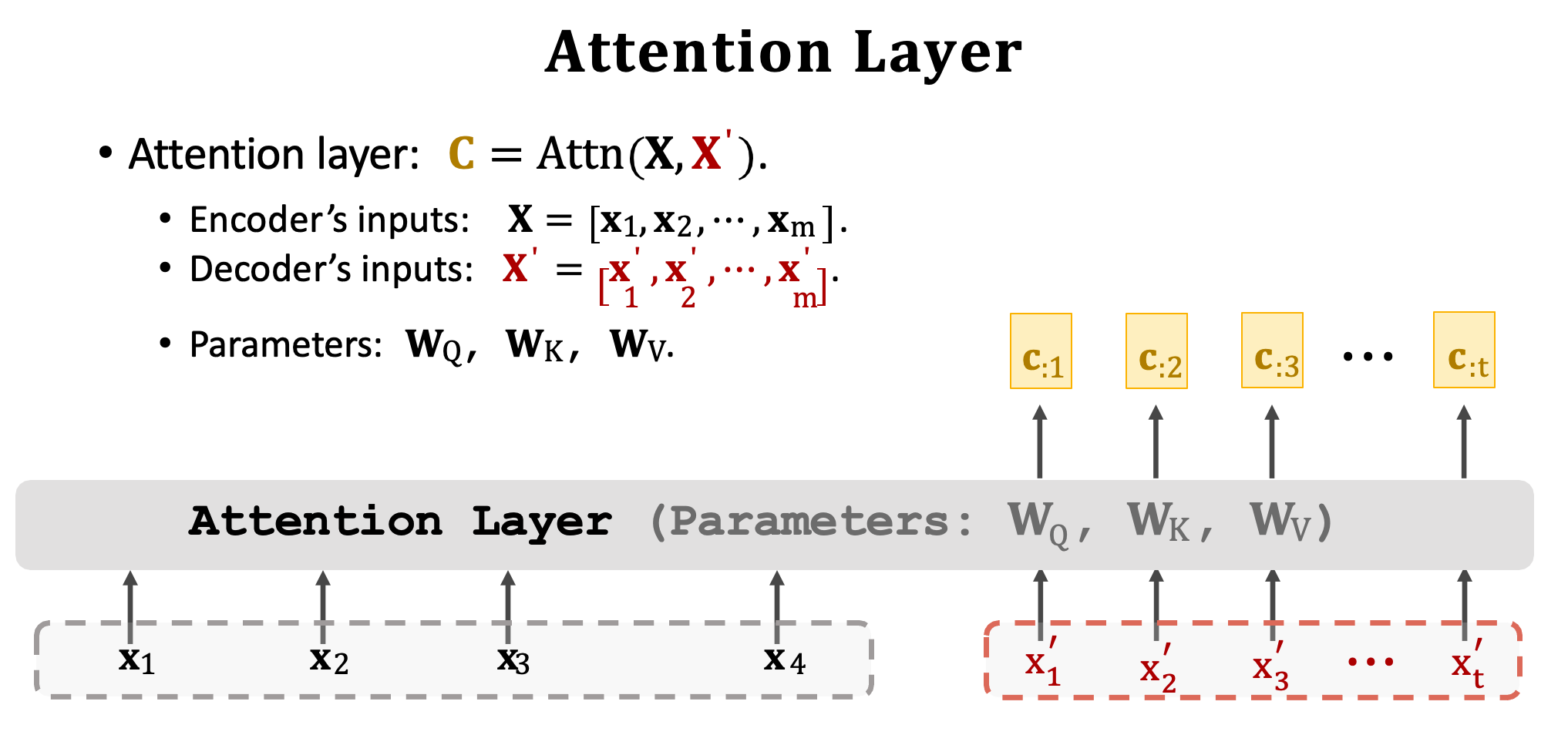
首先我們先設計一個 Attention Layer 用於 Seq2seq 模型，一樣包含一個 Encoder 與一個 Decoder。Encoder 的輸入向量是 x₁~x_m。Decoder 的輸入是 x’1~x’t。

這裡我們捨去 RNN 只用 Attention。首先拿 Encoder 的輸入 x₁~x_m 來計算 Key 與 Value 向量。於是 x₁ 就被映射成 k₁ 與 v₁，x2 就被映射成 k₂ 與 v₂，依此類推我們就得到 m 組的 k 和 v 向量。

然後把 Decoder 的輸入 x’₁~x’_t 做一個線性轉換乘上 Wq 得到 Query。若 Decoder 有 t 個輸入向量，則將會有 t 個 query q₁~q_t。注意一下目前為止總共出現了三個 W 矩陣，分別為 Encoder 中的 W_K 和 W_V 與 Decoder 中的 W_Q。這些權重都是可以經由訓練資料進行學習的權重。

現在開始計算分數𝛂，拿取 Decoder 中的第一個 q₁ 與所有 Encoder 中 m 個 k 向量做對比。透過 Scaled dot product 計算出每一個輸入的分數，也就是所謂的 Attention 關聯強度。我們將會得到 m 維的向量 𝛂1(𝛂₁₁~𝛂_m1)，裏面代表著每個相對應輸入的注意力程度。

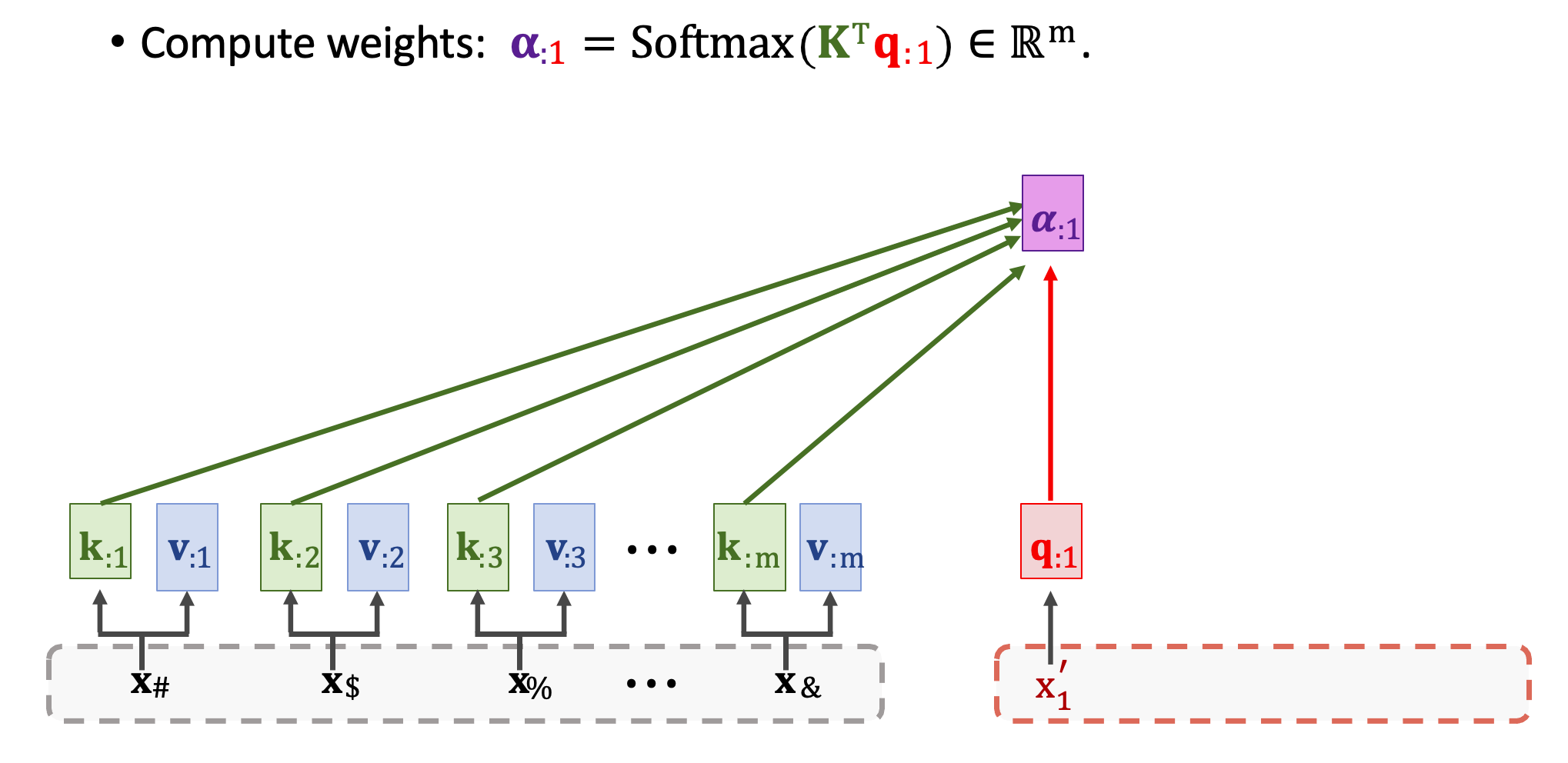
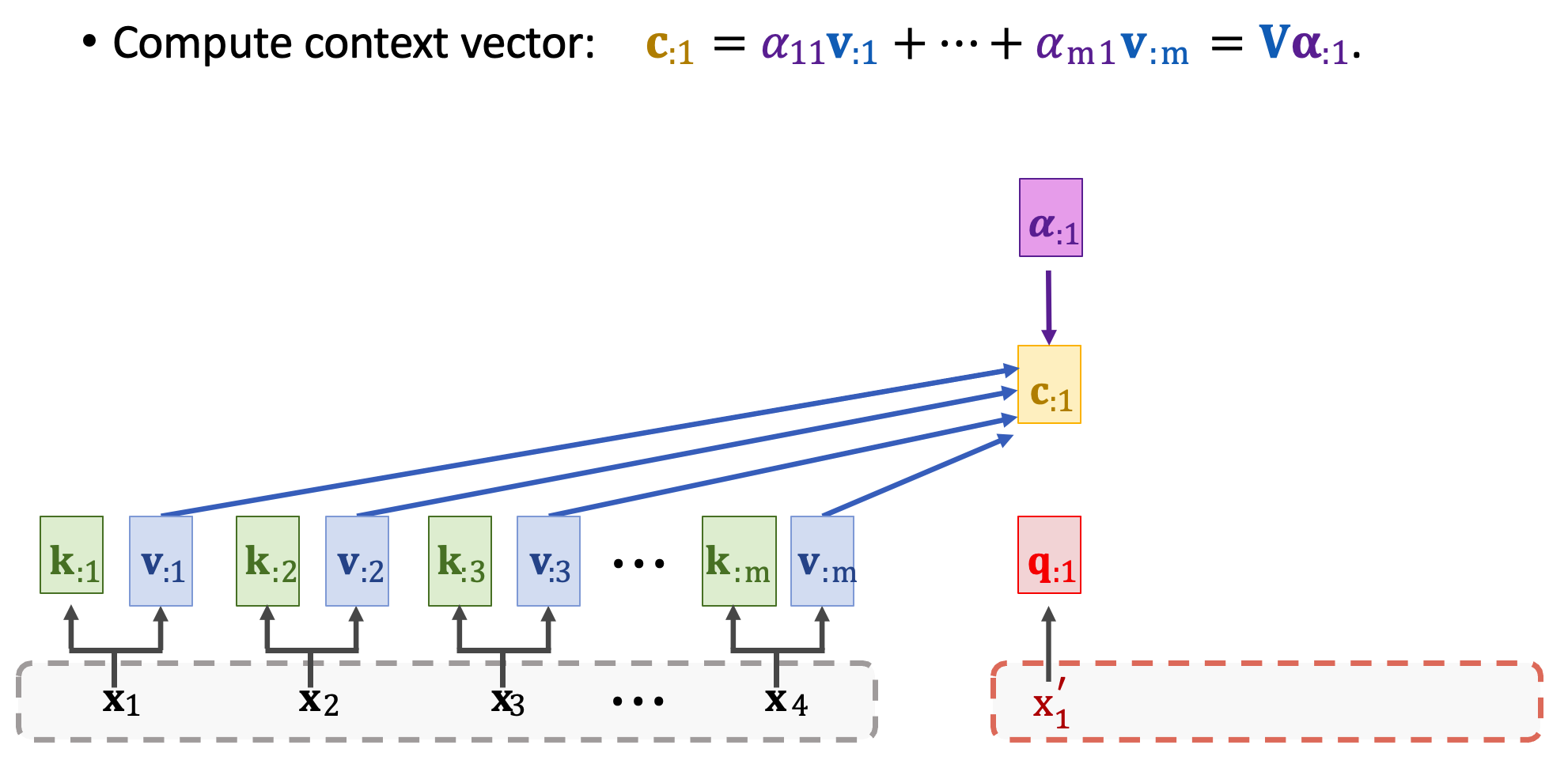
然後再計算 context vector c₁，需要用到分數向量 𝜶₁ 與所有 m 個 value 向量進行加權和。又可以寫成 V𝜶₁。

接下來重複上述步驟可以得到所有 context vector，每一個 c 對應一個 x’。

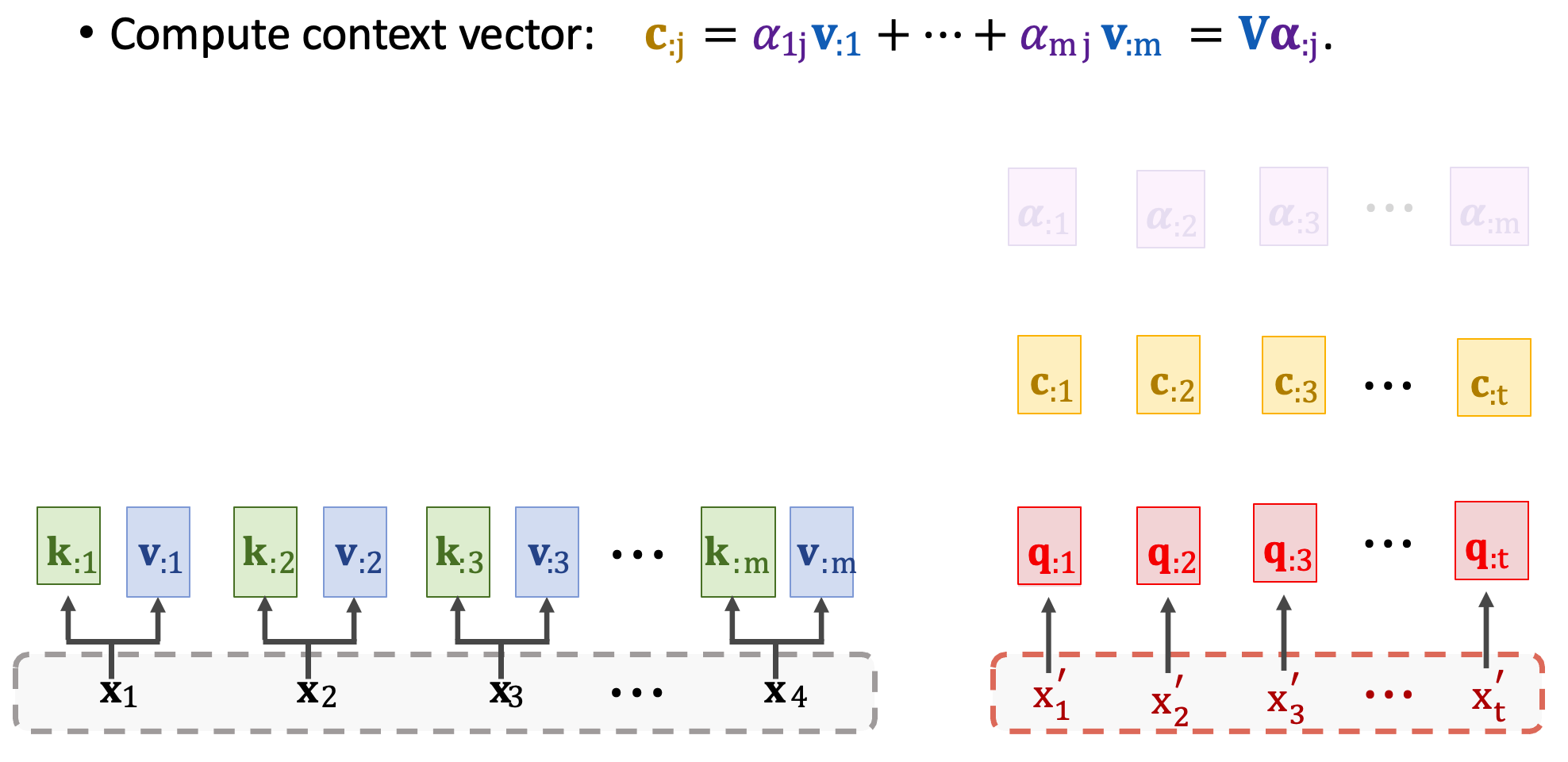
假設有七個輸出將會有七個 context vector，分別為 c₁~c₇ 為最終的輸出。並且可以用 C 表示這些向量。想要計算一個向量 c_j 要用到所有的 Q、K、V。所以 c₂ 依賴於 x’₂ 以及 Encoder 中所有的輸入，並透過注意力分數來取捨資訊。

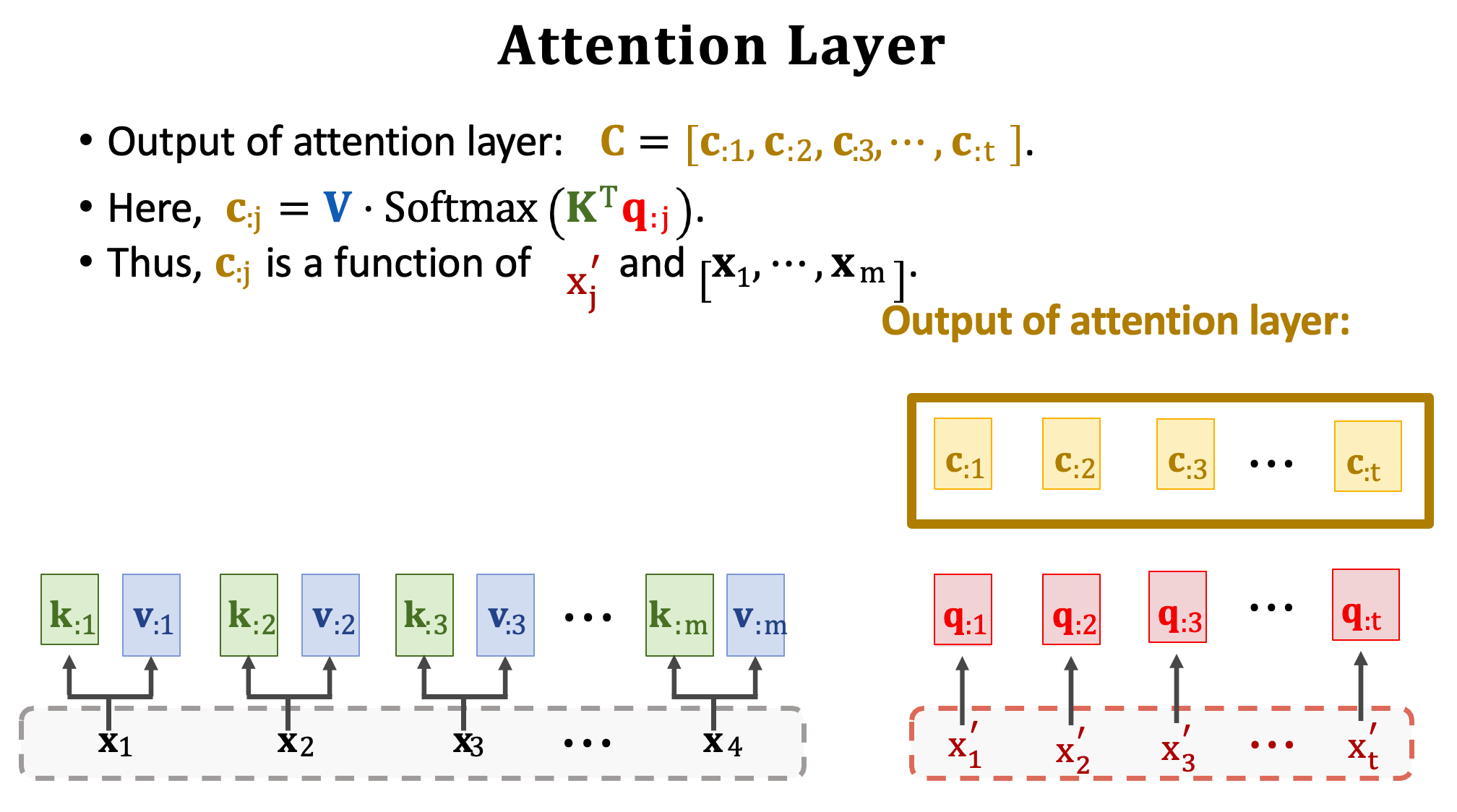
我們把 Attention layer 稱之為函數 Attn()，輸入是分別是 Encoder 的 x₁~x_m (X)以及 Decoder 的 x’₁~x’_t (X’)。除此之外 Attention layer 有三個要學習的權重矩陣 W_Q、W_K、W_V。最後 Attention layer 的輸出是 c₁~c_t (C) 共 t 個向量。因此我們可以總結 Attention layer 有兩個輸入 X 與 X‘，以及一個輸出 C，每一個 c 向量對應一個 x’ 向量。

Self-Attention without RNN

剛才我們將 Seq2seq 模型剔除了 RNN，並採用 Attention Layer 替代。接下來要來了解 Self-Attention Layer。基本上原理完全一模一樣，我們可以使用 Self-Attention 來取代 RNN。

Self-Attention Layer

Self-Attention Layer 並非 Seq2seq 它僅有一個輸入序列，同時可以使用 Attn() 函數表示。此函數跟先前提的方法一模一樣，差別在於函數的輸入都是 X。此外輸出的序列是 c₁~c_m 與輸入 x 的虛列長度是一樣的都是 m，每一個 c 向量都對應一個 x 向量。但是必須注意，舉例來說 c₂ 並非只依賴於 x₂，他是依賴於 x₁~x_m 也就是每個輸入都會考慮過才算出 c₂。

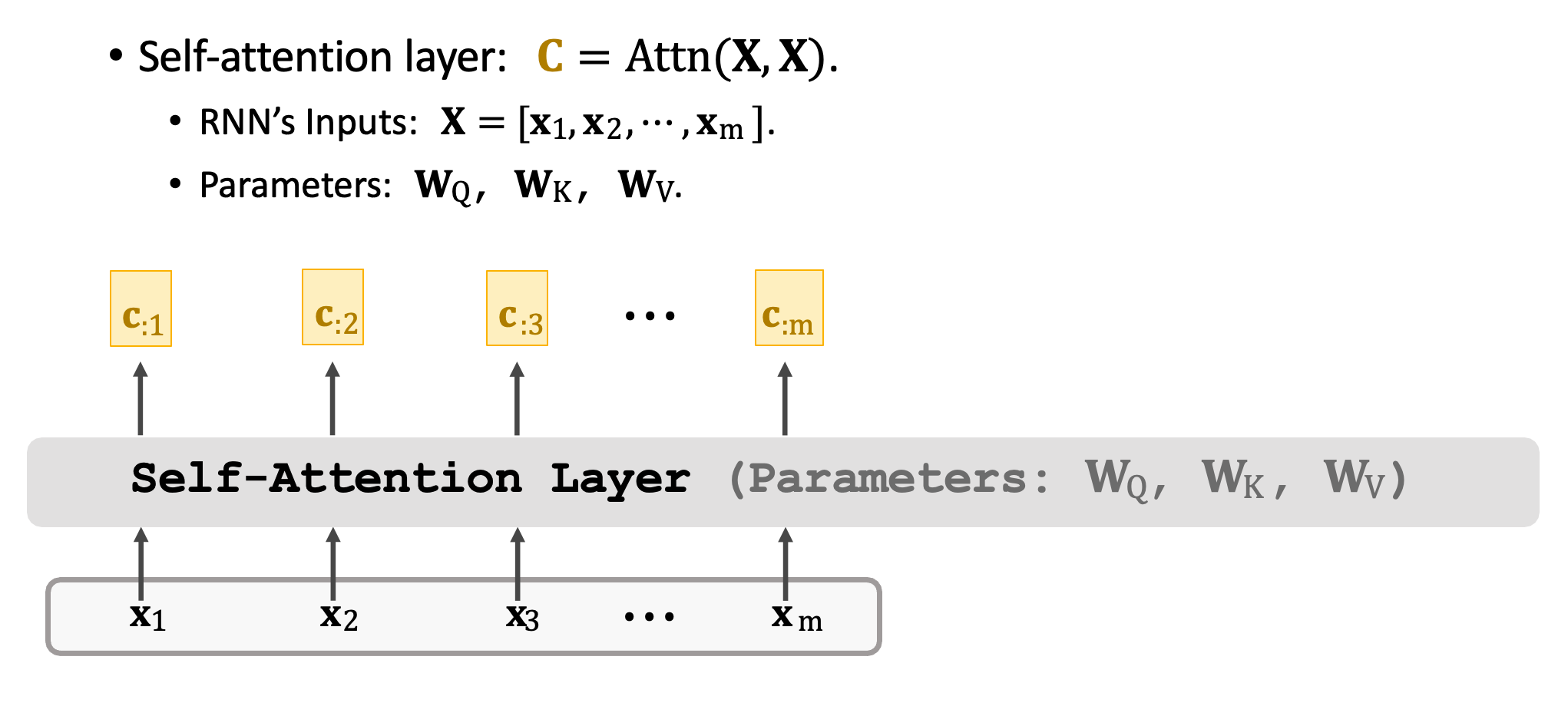
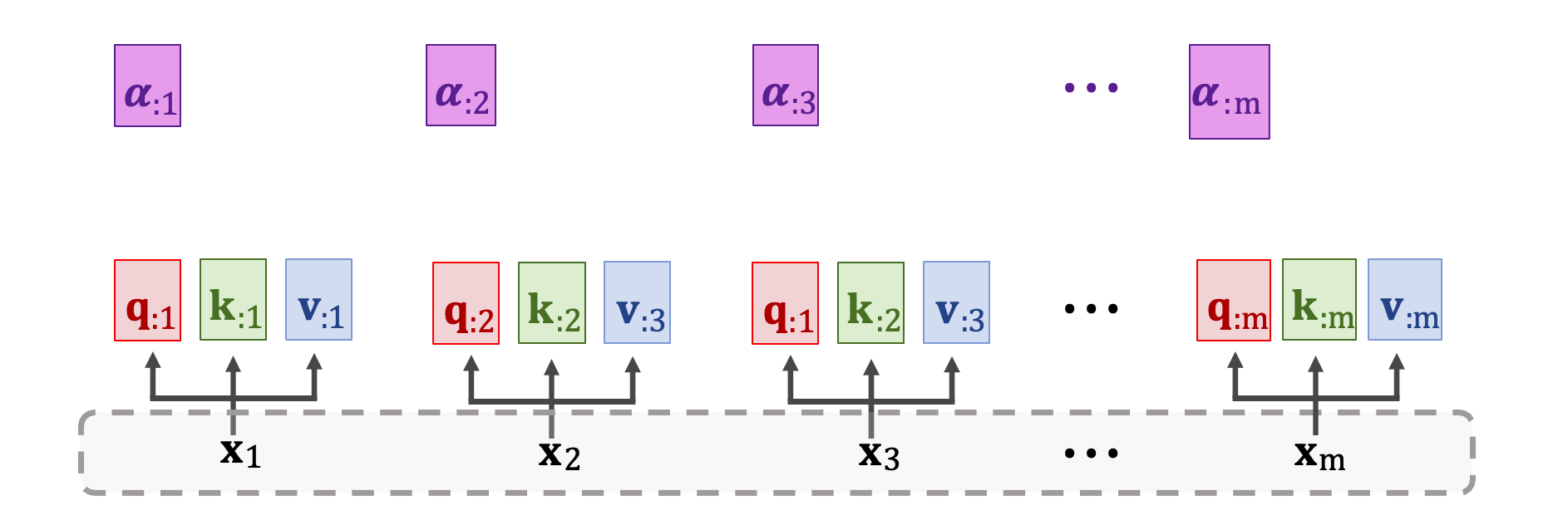
Self-Attention Layer 的原理跟 Attention Layer 完全一模一樣。只差別於輸入不同，在 Self-Attention 中僅有一個輸入序列 x₁~x_m。第一步是做三種轉換將 x_i 映射到 q_i、k_i、v_i 並得到三個向量。權重矩陣依然是 W_Q、W_K、W_V 對輸入 x 做線性轉換。

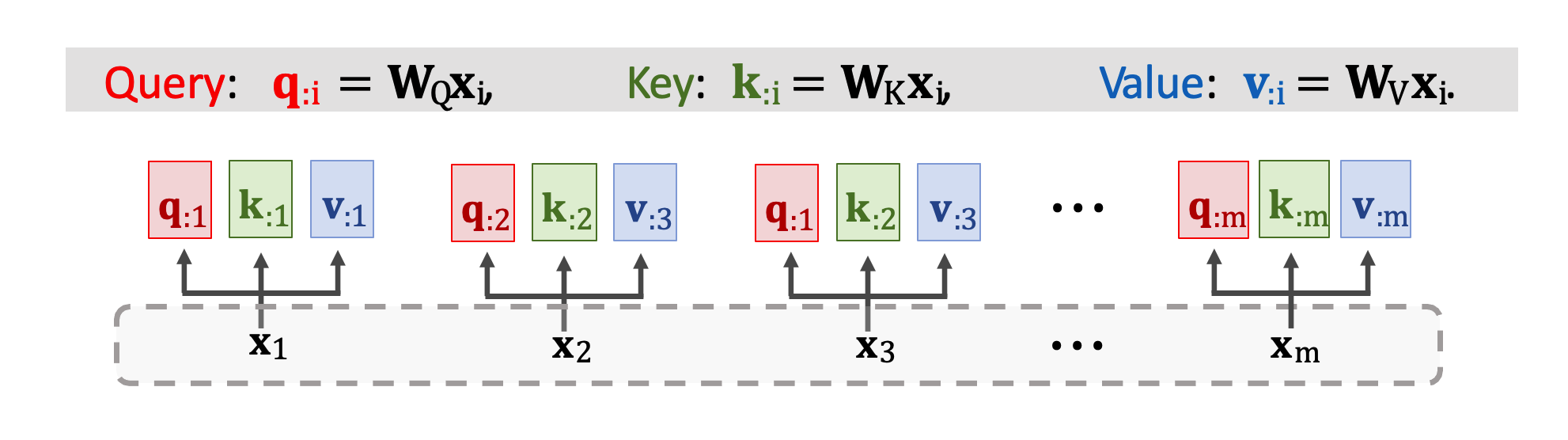
每個 x 輸入都做了線性轉換後會得到 q、k、v 三個向量。接下來再計算分數向量 𝛼 ，公式還是一樣的。我們將矩陣 K(k₁~k_m) 轉置乘上 q_j 向量然後做 Softmax 得到 m 維向量 𝛼_j。我們可以從圖中的例子看到 𝛼₁ 依賴於 q₁ 以及所有 k 向量 k₁~k_m。

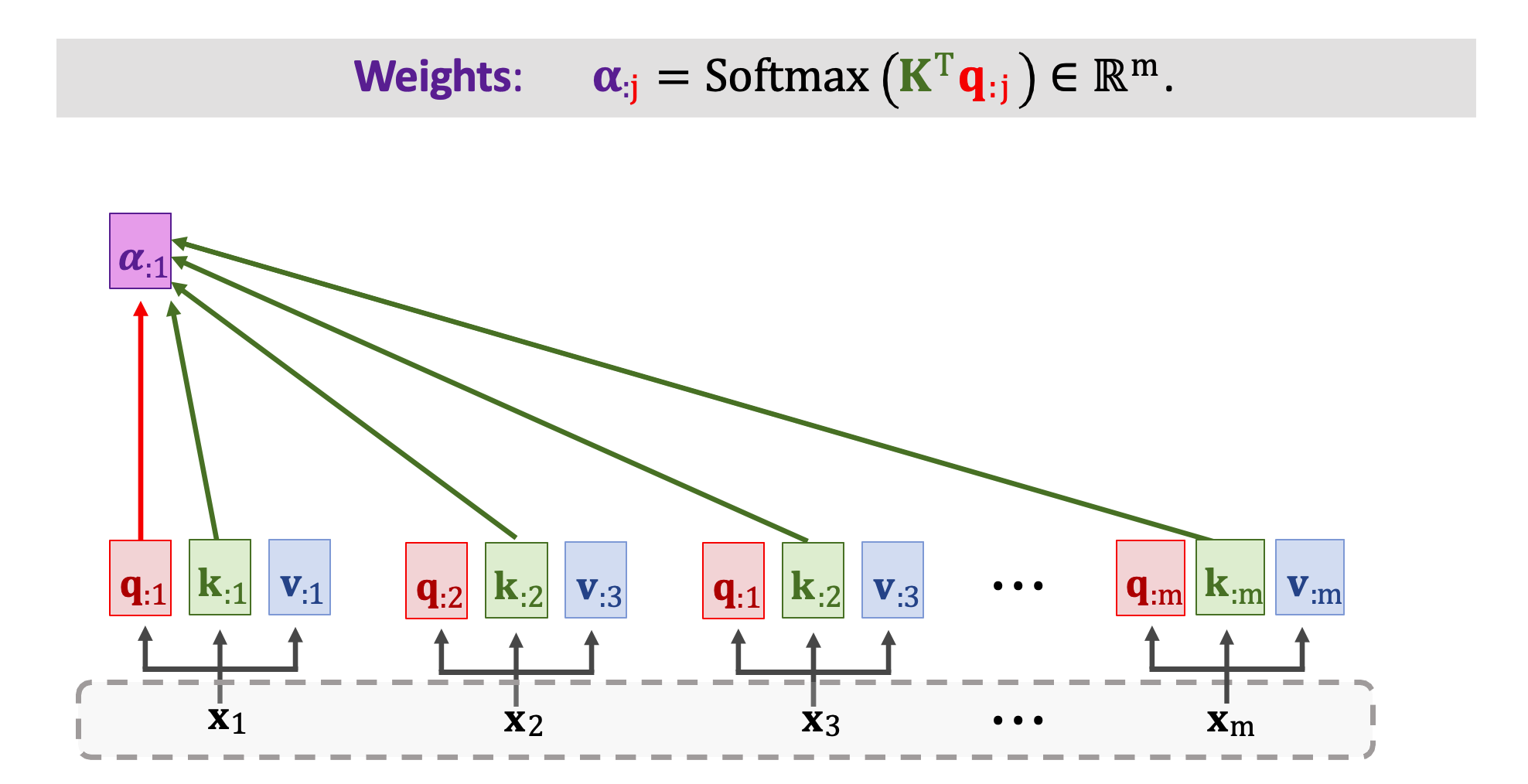
依此類推 𝛼₂ 依賴於 q₂ 以及所有 k 向量 k₁~k_m。用同樣的公式計算出所有分數向量 𝛼。總共有 m 個 𝛼 向量，此外每個分數向量都是 m 維的。

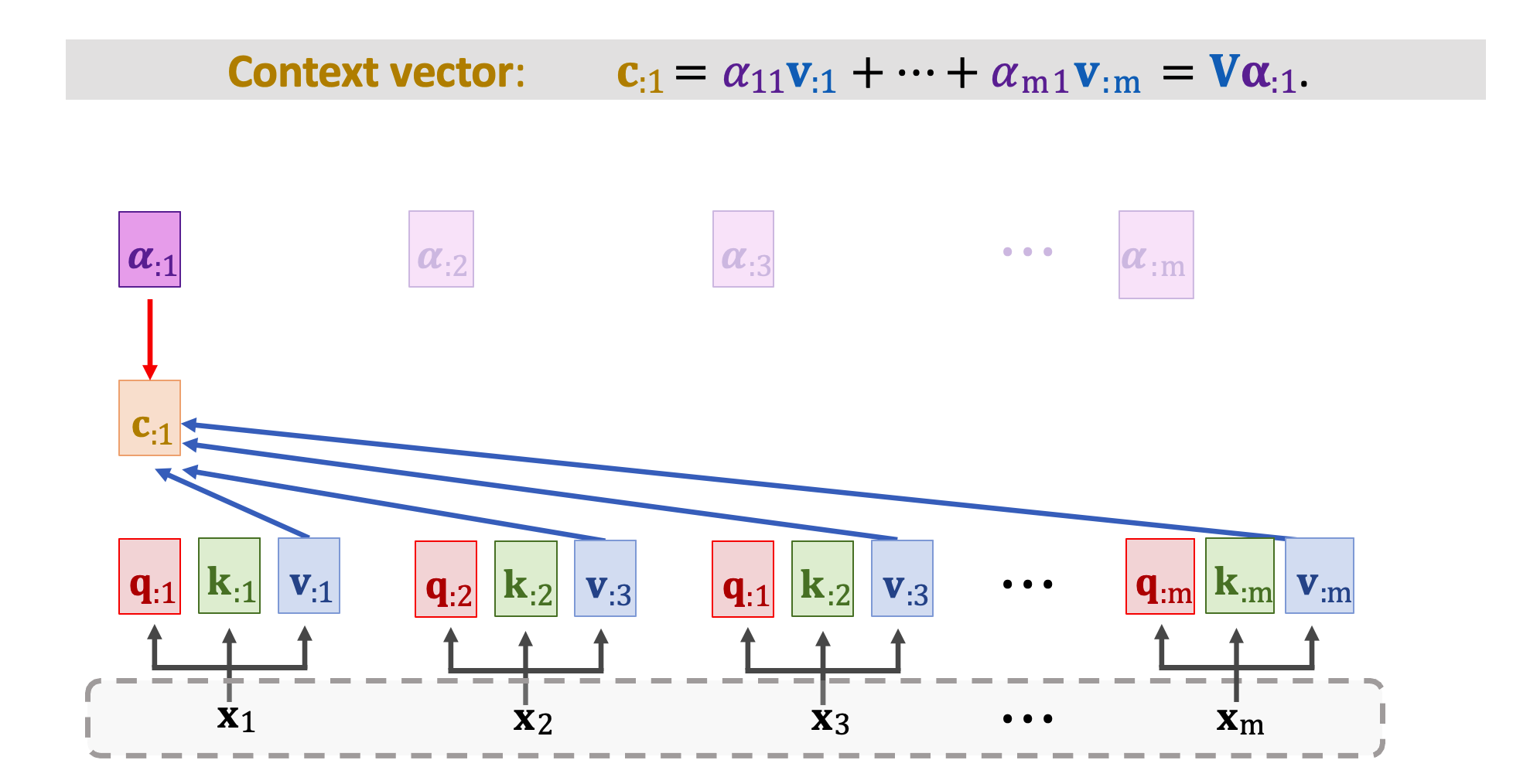
現在可以開始計算 context vector。 c₁ 是所有 m 個 v 向量與 𝛼 的加權和。看以下這張圖，c₁ 依賴於分數向量 𝛼₁，以及所有 m 個 v 向量 v₁~v_m。

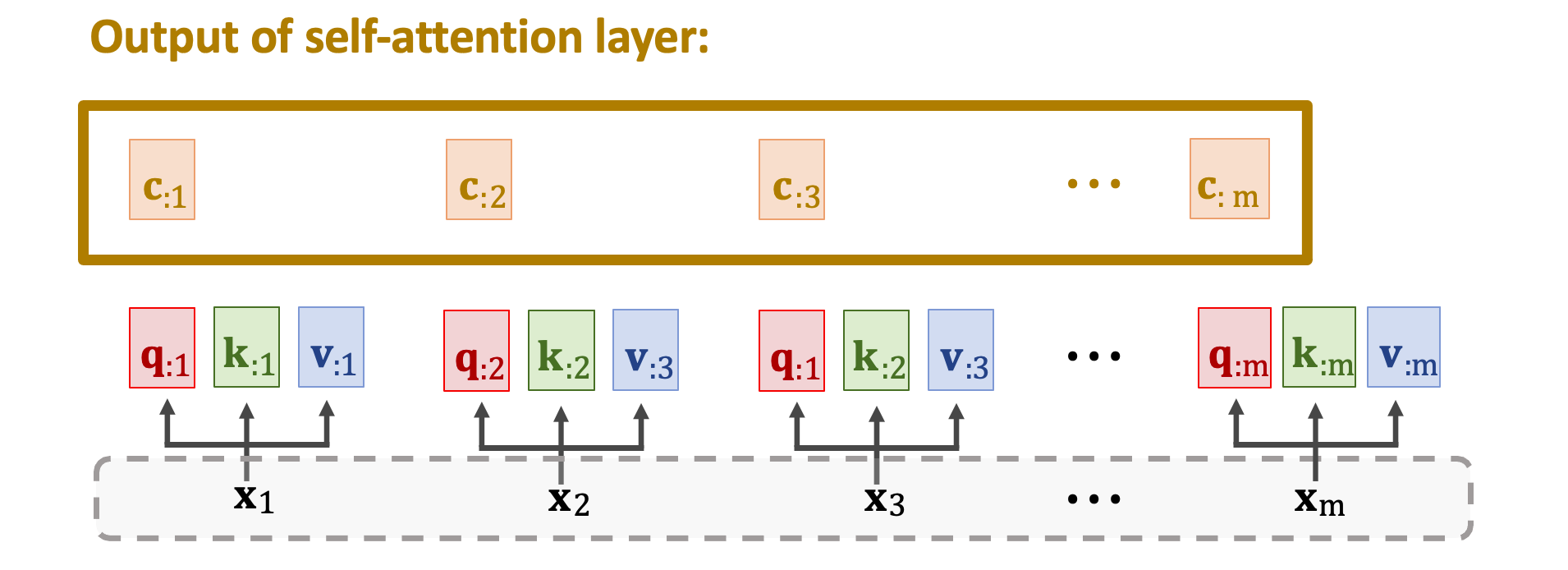
計算同樣的步驟算出 m 個 c 向量得到 c₁~c_m。這 m 個 c 向量就是 Self-Attention Layer 的輸出。其中第 j 個輸出 c_j 是依賴於矩陣 V、K 以及向量 q_j。 因為所有的 c_j 依賴於所有的 K 與 V，所以 c_j 依賴於所有 m 個 x 向量 x₁~x_m。下圖中每個輸入 x_i 位置上都對應一個輸出 c_i，每個 c_i 並非只關注自己的 x_i 而是依賴於所有的 x。只要改變任何一個 x 所有的 c_i 都會發生變化。

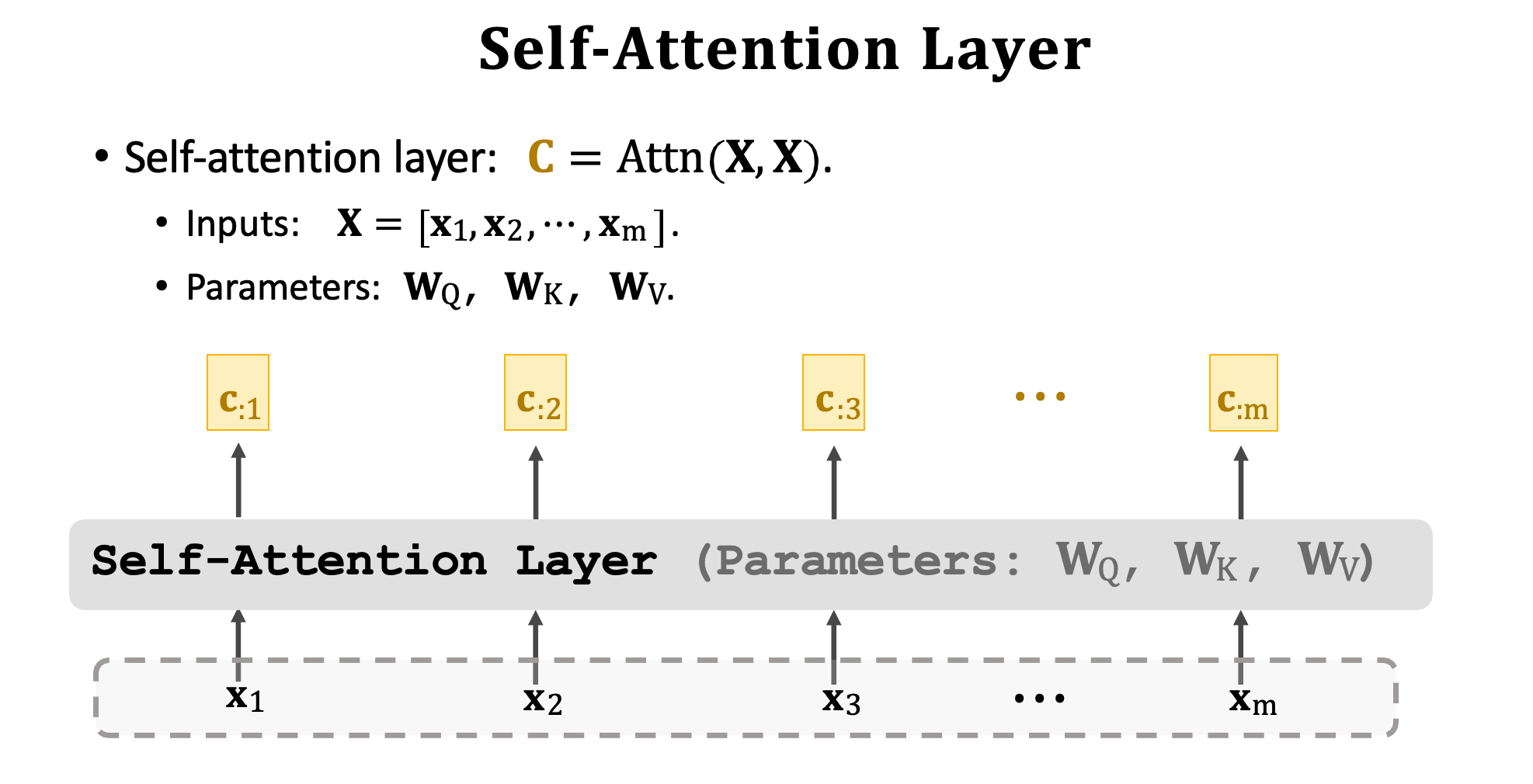
我們已經學習了 Self-Attention Layer 的運作機制。輸入是一個序列 x₁~x_m，這一個網路曾將有三組權重矩陣分別有 W_Q、W_K、W_V。這三個矩陣能把每個 x 映射到 q、k、v 三個向量。其每一個輸出也是一個序列 c₁~c_m 共有 m 個向量，每一個 x 位置上都有對應的 c。 Attention 與 Self-Attention 都用 Attn() 這個函數來表示，此函數有兩個輸入矩陣。Attention Layer 的輸入是 X 與 X’ 而 Self-Attention 的輸入是兩個相同的 X。

小結

到目前為止已經說明了 Attention 與 Self-Attention Layer，最後做一個小結。Attention 的想法最初在 2015 年由 Bengio 實驗室所發表的論文中。此篇論文使用 Attention 改進 Seq2seq 模型，後來大家發現 Attention 並不局限於 Seq2seq 模型，而是可以使用在所有的 RNN 上。如果僅有一個 RNN 網路，那麼 Attention 就稱為 Self-Attention。Self-Attention 這篇論文於 2016 年被發表，再後來 Google 於 2017 年發表的 Attention Is All You Need 表示根本不需要使用到 RNN。直接單獨使用 Attention 效果會更好。另外此篇論文中提出了 Transformer 模型架構，也就是下篇文章將提到的部分。

本篇文章內容來至於線上課程 CS583: Deep Learning

Reference

[1] Bahdanau, Cho, & Bengio. Neural machine translation by jointly learning to align and translate. In ICLR, 2015.

[2] Cheng, Dong, & Lapata. Long Short-Term Memory-Networks for Machine Reading. In EMNLP, 2016.

[3] Vaswani et al. Attention Is All You Need. In NIPS, 2017.

Transformer模型(1/2): 剝離RNN，保留Attention

簡報

版主10在2020年首次開設YouTube頻道，嘗試拍攝程式教學。想要了解更多的朋友歡迎關注我的頻道，您的訂閱就是最大的支持～如果想學其他什麼內容也歡迎許願XD
https://www.youtube.com/channel/UCSNPCGvMYEV-yIXAVt3FA5A