前言

Data Preprocessing(資料前處理)，是機器學習中最重要的一部分。本篇文章中可分為兩部份，前半部份算是一些對資料的觀察、分析(EDA)，後半部主要是針對特徵x進行離群值處理。

資料觀察

這筆數據是隨機產生的資料集，共有2998筆數據，特徵 x 僅有一個。

• 資料筆數： 2998
• 特徵數： 1

# 查看資料分布狀況
data.describe()

count	2998.000000
mean	0.797100
std	    0.091927
min	    0.333300
25%	    0.750000
50%	    0.803750
75%	    0.864825
max	    0.960000

箱型圖

透過 boxplot 來查看特徵 x 在 3143 筆資料中的分布狀況，我們可以看出平均值約 0.8，最大值接近 1，最小值接近 0。其中值大多介於0.6~1之間，其大的數目屬於零星的數量。

plt.figure(figsize=(2,5))
plt.boxplot(data['x'],showmeans=True)
plt.title('x')
plt.show()

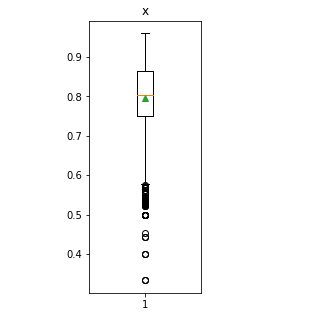
分布狀態

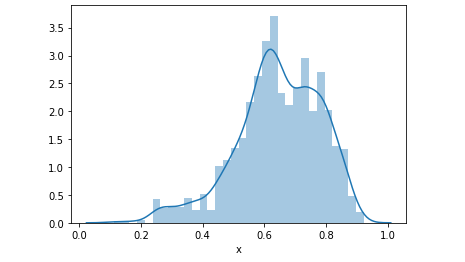
從分布狀態與和密度估計圖可以發現，特徵 x 有左偏的情形。左偏(負偏)，表示有少數幾筆資料很小，故平均數<中位數，所以偏態係數SK<0。

import seaborn as sns
sns.distplot(data['x'])
plt.show()

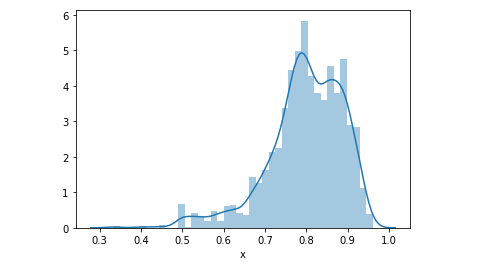
偏態&峰度

#skewness and kurtosis
print("偏態(Skewness): {:.2f}".format(data['x'].skew()))
print("峰度(Kurtosis): {:.2f}".format(data['x'].kurt()))

偏態(Skewness): -1.09
峰度(Kurtosis): 1.80

• 中間圖右偏(正偏)，表示有少數幾筆資料很大，故平均 數>中位數，所以偏態係數SK>0。
• 右邊圖左偏(負偏)，表示有少數幾筆資料很小，故平均 數<中位數，所以偏態係數SK<0。

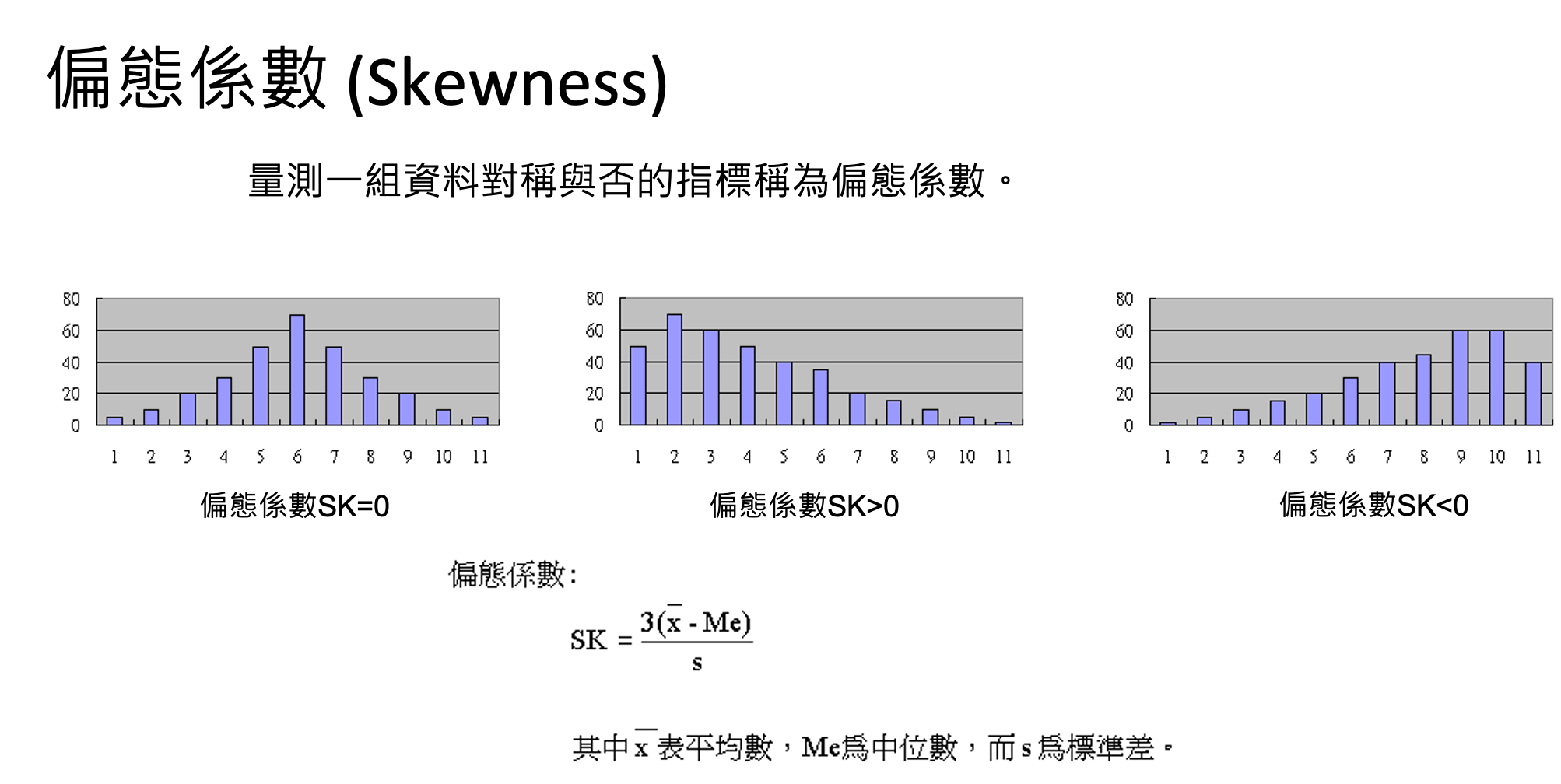
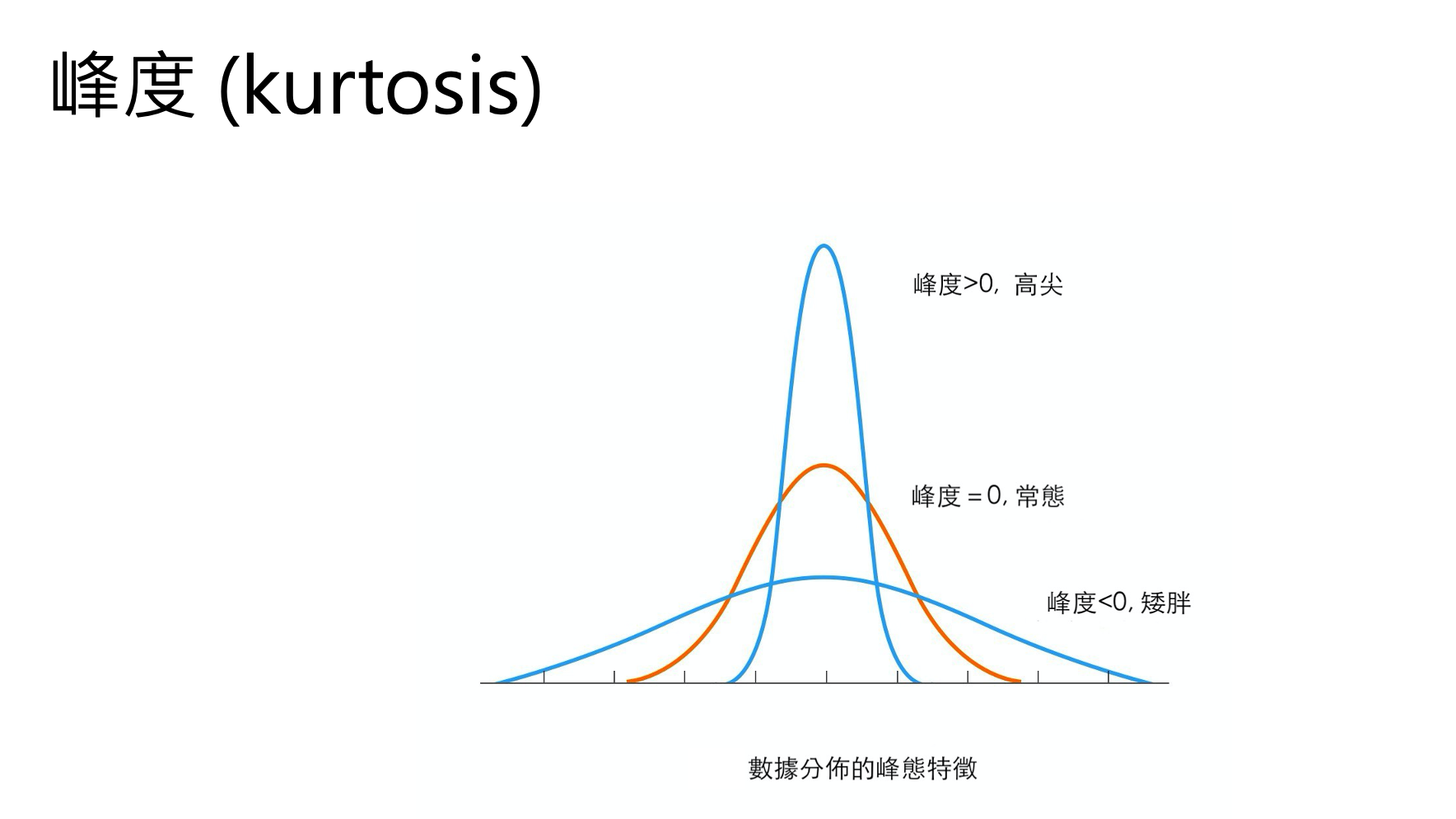
離群值處理

這裡提供兩種常見的方法來對資料進行處理，第一個是將左偏的資料取平方。第二種是透過分位數來移除離群值。

方法1: 特徵取平方

因為資料型態左偏，因此我們可以透過取平方來將資料拉回使為更集中。

exp_data = np.power(data['x'], 2)
exp_data = exp_data.replace([np.inf, -np.inf, -0], 0)
sns.distplot(exp_data)
plt.show()

偏態(Skewness): -0.64

處理右偏的資料可以參考這篇文章

方法二: 移除離群值

在Q3＋1.5IQR（四分位距）和Q1-1.5IQR處畫兩條與中位線一樣的線段，這兩條線段為異常值截斷點，稱其為內限；在Q3＋3IQR和Q1－3IQR處畫兩條線段，稱其為外限。處於內限以外位置的點表示的數據都是異常值，其中在內限與外限之間的異常值為溫和的異常值（mild outliers），在外限以外的為極端的異常值 (extreme outliers)。

參考來源

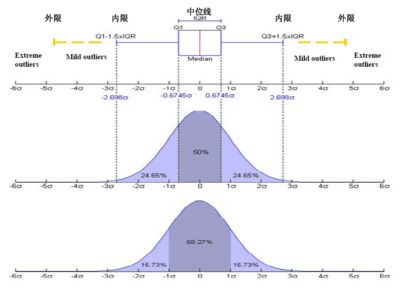
因此我們必須將超出1.5倍的離群值清掉。

print ("Shape Of The Before Ouliers: ",data.shape)
n=1.5
#IQR = Q3-Q1
IQR = np.percentile(data['x'],75) - np.percentile(data['x'],25)
#outlier = Q3 + n*IQR 
data=data[data['x'] < np.percentile(data['x'],75)+n*IQR]
#outlier = Q1 - n*IQR 
data=data[data['x'] > np.percentile(data['x'],25)-n*IQR]
print ("Shape Of The After Ouliers: ",data.shape)

Shape Of The Before Ouliers:  (2998, 1)
Shape Of The After Ouliers:  (2897, 1)

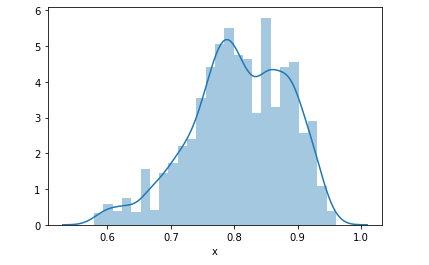
偏態(Skewness): -0.46

完整 Code 可以從我的 GitHub 中取得！

版主10在2020年首次開設YouTube頻道，嘗試拍攝程式教學。想要了解更多的朋友歡迎關注我的頻道，您的訂閱就是最大的支持～如果想學其他什麼內容也歡迎許願XD
https://www.youtube.com/channel/UCSNPCGvMYEV-yIXAVt3FA5A